Computational Materials Science
Computational materials science involves computational tools for solving materials related problems. There exist different mathematical models for investigating problems at multiple length and time scales which help in understanding evolution of material structures (at different length scales) and how these structures effectively control material properties. With this understanding we can select materials for specific applications and also design advanced materials for new applications. At electronic level, Density Functional Theory (DFT) is a popular computational tool while Molecular Dynamics (MD) and Monte Carlo (MC) methods are considered as preferred tools for atomistic simulations. Phase-field Method (PFM) is frequently used for materials problems at micron and mesoscale (between micro and nano) regimes. It helps in understanding temporal evolution of microstructures at these length scales. There are also different models related to solid mechanics, transport phenomena etc. for calculation at continuum level. Finite Element Method (FEM) is most useful computational technique for materials related calculation at structural level. There often exist material problems which have important features at multiple length scales. Multiscale modeling technique is often used for such problems. It involves exchange of information between computational tools at different length scales. These models also take input from thermodynamic and kinetic databases for making quantitative predictions.
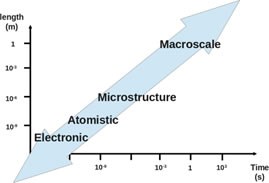
Fig1. Materials related problems at multiple using Phase-field method

Fig2. An example of microstructure length and time scales (spinodal decomposition) modeling
