---

LAB 4 - Finding areas using Randomized algorithms ;
Prime numbers

---

This lab asks you to implements several classes involving loops and iterations.

A. class Triangle

• This class extends lab3 to implement a triangle. Triangles take three points v1, v2, v3 as instance variables, and are defined using a constructor : Triangle (Point v1, Point v2, Point v3)
  NOTE: The constructor must take arguments called v1, v2, v3 and define instance variables of the same name.
  You should also define some more constructors, e.g. default (no arguments), or to take six double arguments (for easier testing).

• The constructor must call a routine draw() which draws the triangle as a set of three drawLine()s.

• Next, you will need to define a method boolean isWithin(Point p) which returns true if the point is in the triangle (not on or outside; be sure to use an EPSILON).

• Using this you will find the area of the triangle using a randomized algorithm: double areaRandomized(int numPoints) This method randomly generates a point inside the canvas area of Lab3, and then finds the area of a given triangle by testing whether the point is inside or outside. It does this for numPoints random points.

• A routine : static void testRandom(int maxTries) : should call this routine repeatedly upto maxTries attempts, with gradually increasing number of random points, to see how the area approaches the precisely computed area,

  Finally, a method that returns the precise area, found using any triangle area method :

  double areaExact()
  

  
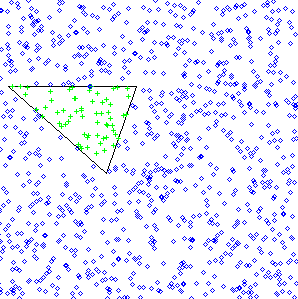
  Based on the points Inside (green "pluses")
  the MonteCarlo computed Area= 5580.0
  whereas the Exact Area is 5605.
  Does this estimate improve if you use
  a much smaller EPSILON for ON?

• Optionally, you should define a method : static void testTriangle(int maxTries) : which generates nTries random triangles, and tests it using areaRandomized() and areaExact()

  HINT: for Triangle.isWithin(): One algorithm for this would be to invoke the Line class of lab3. Here you would define each of the edges as a directed line, and if its equation is

  f(x) = mx - ly + c = 0, then you plug in to this equation points p and the third vertex (that is not on the line). This is similar to the Line.isOn() method of lab 3. If these two values - i.e. f(p) and f(other-vertex) are the same sign, then p is on the same side of this edge as the third vertex. If this is true for all edges then it is INSIDE. If it is ON the edge, it is not IN.

  A more efficient computation to determine whether a point p is to the left or right of the edge joining v1 and v2 is to compute the determinant

  |  v1.x  v1.y 1  |
  |  v2.x  v2.y 1  |
  |  p.x   p.y  1  |
  

  and if it is the same sign for all vertex-pairs, then p is INSIDE; if one case is zero and the other two are same, it is ON etc.

  NOTE: Can we compute the determinant using only two multiplications?

  ---

  B. Class PrimeNums()

  The class PrimeNums() is meant as a simple exercise in looping constructs. It deals with Prime Numbers - first it has a method static boolean isPrime (int n) which returns true if n is a prime number. A sample algorithm is given in the lecture notes on Control If you can read up on arrays, then you may try to implement the Erastothenes Sieve defined in PrimeNumbers.txt which works far more efficiently using an array of integers. Next it defines the method static void primeDiff (int diff, int maxN) where diff is an even number, and prints all the prime numbers less than maxN such that the difference of the two primes is exactly equal to diff.

  ---